23.1 Growing a minimum spanning tree

Assume that we have a connected, undirected graph G = (V, E) with a weight function w : E → R, and we wish to find a minimum spanning tree for G. The two algorithms we consider in this chapter use a greedy approach to the problem, although they differ in how they apply this approach.

This greedy strategy is captured by the following "generic" algorithm, which grows the minimum spanning tree one edge at a time. The algorithm manages a set of edges A, maintaining the following loop invariant:

Prior to each iteration, A is a subset of some minimum spanning tree.

At each step, we determine an edge (u, v) that can be added to A without violating this invariant, in the sense that A∪{(u, v)} is also a subset of a minimum spanning tree. We call such an edge a safe edge for A, since it can be safely added to A while maintaining the invariant.

GENERIC-MST(G, w)
1  A ← Ø
2  while A does not form a spanning tree
3      do find an edge (u, v) that is safe for A
4          A ← A ∪ {(u, v)}
5  return A

We use the loop invariant as follows:

Initialization: After line 1, the set A trivially satisfies the loop invariant.
Maintenance: The loop in lines 2-4 maintains the invariant by adding only safe edges.
Termination: All edges added to A are in a minimum spanning tree, and so the set A is returned in line 5 must be a minimum spanning tree.

The tricky part is, of course, finding a safe edge in line 3. One must exist, since when line 3 is executed, the invariant dictates that there is a spanning tree T such that A ⊆ T. Within the while loop body, A must be a proper subset of T, and therefore there must be an edge (u, v) ∈ T such that (u, v) ∉ A and (u, v) is safe for A.

In the remainder of this section, we provide a rule (Theorem 23.1) for recognizing safe edges. The next section describes two algorithms that use this rule to find safe edges efficiently.

We first need some definitions. A cut (S, V - S) of an undirected graph G = (V, E) is a partition of V. Figure 23.2 illustrates this notion. We say that an edge (u, v) ∈ E crosses the cut (S, V - S) if one of its endpoints is in S and the other is in V - S. We say that a cut respects a set A of edges if no edge in A crosses the cut. An edge is a light edge crossing a cut if its weight is the minimum of any edge crossing the cut. Note that there can be more than one light edge crossing a cut in the case of ties. More generally, we say that an edge is a light edge satisfying a given property if its weight is the minimum of any edge satisfying the property.

Figure 23.2: Two ways of viewing a cut (S, V - S) of the graph from Figure 23.1. (a) The vertices in the set S are shown in black, and those in V - S are shown in white. The edges crossing the cut are those connecting white vertices with black vertices. The edge (d, c) is the unique light edge crossing the cut. A subset A of the edges is shaded; note that the cut (S, V - S) respects A, since no edge of A crosses the cut. (b) The same graph with the vertices in the set S on the left and the vertices in the set V - S on the right. An edge crosses the cut if it connects a vertex on the left with a vertex on the right.

Our rule for recognizing safe edges is given by the following theorem.

Theorem 23.1

Let G = (V, E) be a connected, undirected graph with a real-valued weight function w defined on E. Let A be a subset of E that is included in some minimum spanning tree for G, let (S, V - S) be any cut of G that respects A, and let (u, v) be a light edge crossing (S, V - S). Then, edge (u, v) is safe for A.

Proof Let T be a minimum spanning tree that includes A, and assume that T does not contain the light edge (u, v), since if it does, we are done. We shall construct another minimum spanning tree T′ that includes A ∪{(u, v)} by using a cut-and-paste technique, thereby showing that (u, v) is a safe edge for A.

The edge (u, v) forms a cycle with the edges on the path p from u to v in T, as illustrated in Figure 23.3. Since u and v are on opposite sides of the cut (S, V - S), there is at least one edge in T on the path p that also crosses the cut. Let (x, y) be any such edge. The edge (x, y) is not in A, because the cut respects A. Since (x, y) is on the unique path from u to v in T, removing (x, y) breaks T into two components. Adding (u, v) reconnects them to form a new spanning tree T′ = T - {(x, y)} ∪ {(u, v)}.

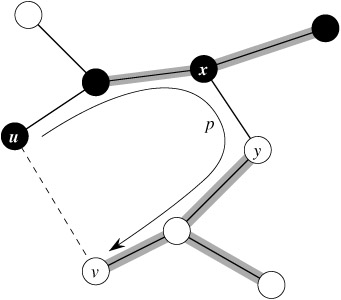
Figure 23.3: The proof of Theorem 23.1. The vertices in S are black, and the vertices in V - S are white. The edges in the minimum spanning tree T are shown, but the edges in the graph G are not. The edges in A are shaded, and (u, v) is a light edge crossing the cut (S, V - S). The edge (x, y) is an edge on the unique path p from u to v in T. A minimum spanning tree T′ that contains (u, v) is formed by removing the edge (x, y) from T and adding the edge (u, v).

We next show that T′ is a minimum spanning tree. Since (u, v) is a light edge crossing (S, V - S) and (x, y) also crosses this cut, w(u, v) ≤ w(x, y). Therefore,

w(T′)	=	w(T - w(x, y) + w(u, v)
	≤	w(T).

But T is a minimum spanning tree, so that w(T) ≤ w(T′); thus, T′ must be a minimum spanning tree also.

It remains to show that (u, v) is actually a safe edge for A. We have A ⊆ T′, since A ⊆ T and (x, y) ∉ A; thus, A ∪ {(u, v)} ⊆ T′. Consequently, since T′ is a minimum spanning tree, (u, v) is safe for A.

Theorem 23.1 gives us a better understanding of the workings of the GENERIC-MST algorithm on a connected graph G = (V, E). As the algorithm proceeds, the set A is always acyclic; otherwise, a minimum spanning tree including A would contain a cycle, which is a contradiction. At any point in the execution of the algorithm, the graph G_A = (V, A) is a forest, and each of the connected components of G_A is a tree. (Some of the trees may contain just one vertex, as is the case, for example, when the algorithm begins: A is empty and the forest contains |V| trees, one for each vertex.) Moreover, any safe edge (u, v) for A connects distinct components of G_A, since A ∪ {(u, v)} must be acyclic.

The loop in lines 2-4 of GENERIC-MST is executed |V| - 1 times as each of the |V| - 1 edges of a minimum spanning tree is successively determined. Initially, when A = Ø, there are |V| trees in G_A, and each iteration reduces that number by 1. When the forest contains only a single tree, the algorithm terminates.

The two algorithms in Section 23.2 use the following corollary to Theorem 23.1.

Corollary 23.2

Let G = (V, E) be a connected, undirected graph with a real-valued weight function w defined on E. Let A be a subset of E that is included in some minimum spanning tree for G, and let C = (V_C, E_C) be a connected component (tree) in the forest G_A = (V, A). If (u, v) is a light edge connecting C to some other component in G_A, then (u, v) is safe for A.

Proof The cut (V_C, V - V_C) respects A, and (u, v) is a light edge for this cut. Therefore, (u, v) is safe for A.

Exercises 23.1-1

Let (u, v) be a minimum-weight edge in a graph G. Show that (u, v) belongs to some minimum spanning tree of G.

Exercises 23.1-2

Professor Sabatier conjectures the following converse of Theorem 23.1. Let G = (V, E) be a connected, undirected graph with a real-valued weight function w defined on E. Let A be a subset of E that is included in some minimum spanning tree for G, let (S, V - S) be any cut of G that respects A, and let (u, v) be a safe edge for A crossing (S, V - S). Then, (u, v) is a light edge for the cut. Show that the professor's conjecture is incorrect by giving a counterexample.

Exercises 23.1-3

Show that if an edge (u, v) is contained in some minimum spanning tree, then it is a light edge crossing some cut of the graph.

Exercises 23.1-4

Give a simple example of a graph such that the set of edges {(u, v) : there exists a cut (S, V - S) such that (u, v) is a light edge crossing (S, V - S)} does not form a minimum spanning tree.

Exercises 23.1-5

Let e be a maximum-weight edge on some cycle of G = (V, E). Prove that there is a minimum spanning tree of G′ = (V, E -{e}) that is also a minimum spanning tree of G. That is, there is a minimum spanning tree of G that does not include e.

Exercises 23.1-6

Show that a graph has a unique minimum spanning tree if, for every cut of the graph, there is a unique light edge crossing the cut. Show that the converse is not true by giving a counterexample.

Exercises 23.1-7

Argue that if all edge weights of a graph are positive, then any subset of edges that connects all vertices and has minimum total weight must be a tree. Give an example to show that the same conclusion does not follow if we allow some weights to be nonpositive.

Exercises 23.1-8

Let T be a minimum spanning tree of a graph G, and let L be the sorted list of the edge weights of T. Show that for any other minimum spanning tree T′ of G, the list L is also the sorted list of edge weights of T′.

Exercises 23.1-9

Let T be a minimum spanning tree of a graph G = (V, E), and let V′ be a subset of V. Let T′ be the subgraph of T induced by V′, and let G′ be the subgraph of G induced by V′. Show that if T′ is connected, then T′ is a minimum spanning tree of G′.

Exercises 23.1-10

Given a graph G and a minimum spanning tree T, suppose that we decrease the weight of one of the edges in T. Show that T is still a minimum spanning tree for G. More formally, let T be a minimum spanning tree for G with edge weights given by weight function w. Choose one edge (x, y) ∈ T and a positive number k, and define the weight function w′ by

Show that T is a minimum spanning tree for G with edge weights given by w′.

Exercises 23.1-11: ★

Given a graph G and a minimum spanning tree T, suppose that we decrease the weight of one of the edges not in T. Give an algorithm for finding the minimum spanning tree in the modified graph.