Metoda Aproximatiilor succesive pentru ecuatia x=f(x)

Metoda aproximatiilor succesive

Consideram f(x) = 0 ecuatie algebrica sau transcendenta care are in intervalul [a,b] o singura radacina reala δ. Notam φ(x) = f(x) + x; pentru f(x) = 0 ecuatia devine

x = φ(x). Se observa ca, daca δ este radacina ecuatiei f(x) = 0 atunci ea vafi si radacina ecuatiei x = φ(x).

Se observa ca, daca δ este radacina ecuatiei f(x) = 0 atunci ea va fi si radacina a ecuatiei x = φ(x).

Cunoscand o valoare initiala , metoda aproximatiilor succesive consta intr-un sir de iteratii:

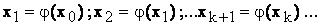
l      Daca φ(x) este derivabila pe [a,b] si, daca, pentru , atunci sirul iteratiilor definit mai sus converge catre δ, radacina unica a ecuatiei f(x) = 0.

Dem. Consideram diferenta careia i se aplica teorema lui Lagrange: , unde

Deoarece pentru

pentru n = 0:

pentru n = 1:

#include <stdio.h>
#include<conio.h>
#include<math.h>
#include <iostream.h>
double x,eps;
int n,ITMAX;
double f(double x){
	return exp(-x);
}
void main(){
	clrscr();
	cout.precision(10);
	cout<<"\nDati aproximatia initiala x=";cin>>x;
	cout<<"\nDati eroare admisa eps=";cin>>eps;
	cout<<"\nDati numarul maxim de iteratii ITMAX=";cin>>ITMAX;
	n=0;
	while ((fabs(x-f(x))>eps)  &&  (n<=ITMAX)){
		x=f(x);
		n++;
	cout<<"\n"<<n<<"  "<<x<<"    |x-f(x)|="<<fabs(x-f(x));
	}
	cout<<"\n";
	if (n>ITMAX)
	   cout<<"\nIn ITMAX iteratii nu a fost relizata aproximarea dorita";
	else
	   {
	   cout<<"\n";
	   cout<<"\nAproximarea obtinuta: x="<<x;
	   cout<<"\n";
	   cout<<"\nEroarea: |x-f(x)|="<<fabs(x-f(x));
	   cout<<"\n";
	   cout<<"\nNumarul de iteratii efectuat: n="<<n;
	   }
	getch();
}

1,408 total views, 2 views today